Lorem ipsum dolor sit amet, consectetur adipisicing elit. Odit molestiae mollitia laudantium assumenda nam eaque, excepturi, soluta, perspiciatis cupiditate sapiente, adipisci quaerat odio voluptates consectetur nulla eveniet iure vitae quibusdam? Excepturi aliquam in iure, repellat, fugiat illum voluptate repellendus blanditiis veritatis ducimus ad ipsa quisquam, commodi vel necessitatibus, harum quos a dignissimos.
Close Save changesHelp F1 or ? Previous Page ← + CTRL (Windows) ← + ⌘ (Mac) Next Page → + CTRL (Windows) → + ⌘ (Mac) Search Site CTRL + SHIFT + F (Windows) ⌘ + ⇧ + F (Mac) Close Message ESC
Earlier in this lesson we learned that the sampling distribution is impacted by sample size. As the sample size increases the standard error decreases. With a larger sample size there is less variation between sample statistics, or in this case bootstrap statistics. Let's look at how this impacts a confidence interval.
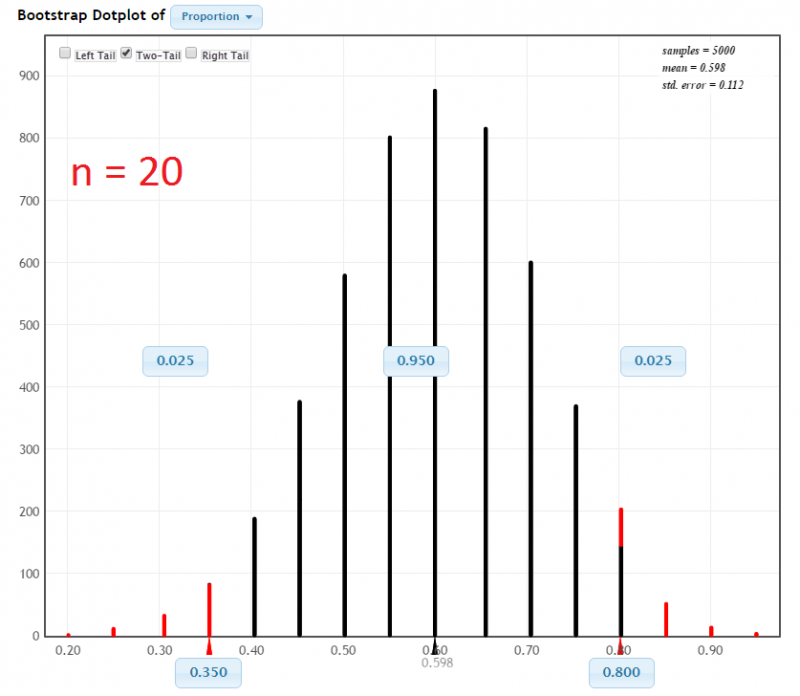
Below are two bootstrap distributions with 95% confidence intervals. In both examples \(\widehat p = 0.60\). However, the sample sizes are different.
In a sample of 20 World Campus students 12 owned a dog. StatKey was used to construct a 95% confidence interval using the percentile method:

In a sample of 200 World Campus students, 120 owned a dog. StatKey was used to construct a 95% confidence interval using the percentile method:
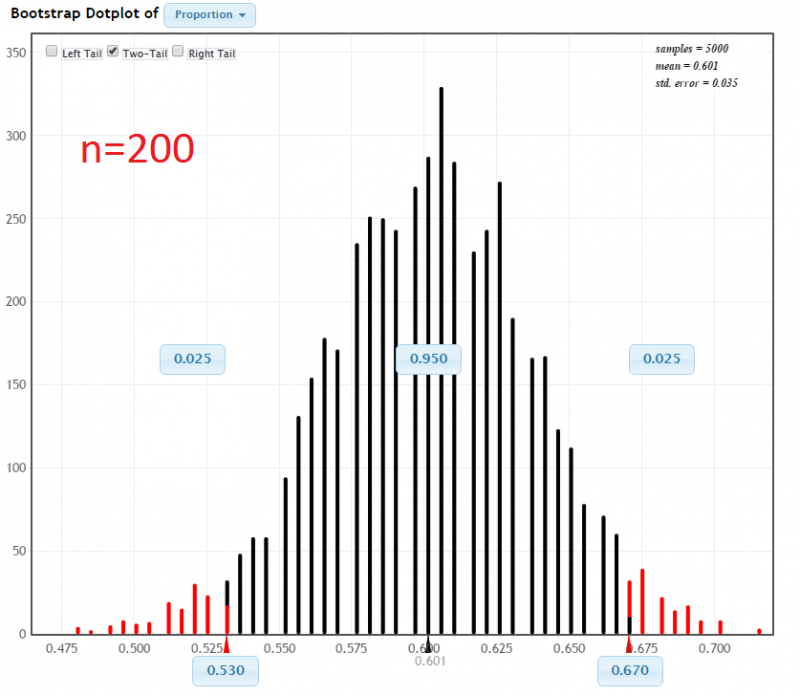
In each of the examples the proportion of dog owners was \(\widehat p = 0.60\). The difference was the sample size. When the sample size was increased from 20 to 200 the confidence interval became more narrow: from [0.350, 0.800] to [0.530, 0.670].